《Weight-Sharing Neural Architecture Search: A Battle to Shrink the Optimization Gap》(2020, 一作华为诺亚方舟实验室 Lingxi Xie, 在 VALSE2020 安利了诺亚的NAS新作 GOLD-NAS)

1 INTRODUCTION

权重共享网络架构搜索：同时从 super-net 中筛选合适的子网络以及子网络的参数。

将权重共享网络架构搜索按照 “搜索空间建模” 和 “搜索策略算法” 分为两大类。

2 NAS

2.1 Overall Framework

NAS 的理想目标函数是：

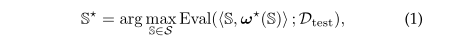
实际的目标函数是：找到一个子网络S使得参数w*在训练集上loss最小，并且S在所有子网络中验证集accuracy最高。

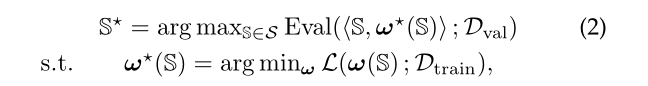
传统NAS算法伪代码：

2.2 Search Space

2.2.1 The EvoNet Search Space

[18] E. Real, S. Moore, A. Selle, S. Saxena, Y. L. Suematsu, J. Tan, Q. V. Le, and A. Kurakin, “Large-scale evolution of image classifiers,” in International Conference on Machine Learning, 2017. (EvoNet)

[42] H. Liu, K. Simonyan, O. Vinyals, C. Fernando, and K. Kavukcuoglu, “Hierarchical representations for efficient architecture search,” in International Conference on Learning Representations, 2018.

[43] L. Wang, S. Xie, T. Li, R. Fonseca, and Y. Tian, “Sample efficient neural architecture search by learning action space,” arXiv preprint arXiv:1906.06832, 2019.

[44] E. Real, C. Liang, D. R. So, and Q. V. Le, “Automl-zero: Evolving machine learning algorithms from scratch,” arXiv preprint arXiv:2003.03384, 2020.

此类工作研究的是完全开放的搜索空间，cell number / cell connections / cell components 等网络结构约束条件一概没有，搜索空间被定义为是 a set of actions on the architecture, e.g., inserting/removing a convolutional layer to a specific position, altering the kernel size of a convolutional layer, adding/deleting a skip connection between two layers 等等。

完全开放的搜索空间是未来的研究趋势，目前存在的挑战是缺少 robust search strategy。

2.2.2 The NAS-RL Search Space

[19] L. Xie and A. Yuille, “Genetic cnn,” in International Conference on Computer Vision, 2017.

[20] B. Zoph and Q. V. Le, “Neural architecture search with reinforcement learning,” in International Conference on Learning Representations, 2017.

此类工作搜索的是 densely-connected macro architecture，存在 \(2^{(N−1)(N−2)/2}\) 种可能。这么来的：

假设每个 cell 里可以有 C 种 operator 的组合方法（包括 filter height, filter width, stride height, stride width, the number of filters），所以全部的搜索空间中有： \(C^N \cdot 2^{(N−1)(N−2)/2}\) 种可能。

2.2.3 The NASNet Search Space

[25] H. Liu, K. Simonyan, and Y. Yang, “Darts: Differentiable architecture search,” in International Conference on Learning Representations, 2019.

[45] B. Zoph, V. Vasudevan, J. Shlens, and Q. V. Le, “Learning transferable architectures for scalable image recognition,” in Computer Vision and Pattern Recognition, 2018.

[46] C. Liu, B. Zoph, M. Neumann, J. Shlens, W. Hua, L.-J. Li, L. FeiFei, A. Yuille, J. Huang, and K. Murphy, “Progressive neural architecture search,” in European Conference on Computer Vision, 2018.

[47] E. Real, A. Aggarwal, Y. Huang, and Q. V. Le, “Regularized evolution for image classifier architecture search,” in AAAI Conference on Artificial Intelligence, 2019.

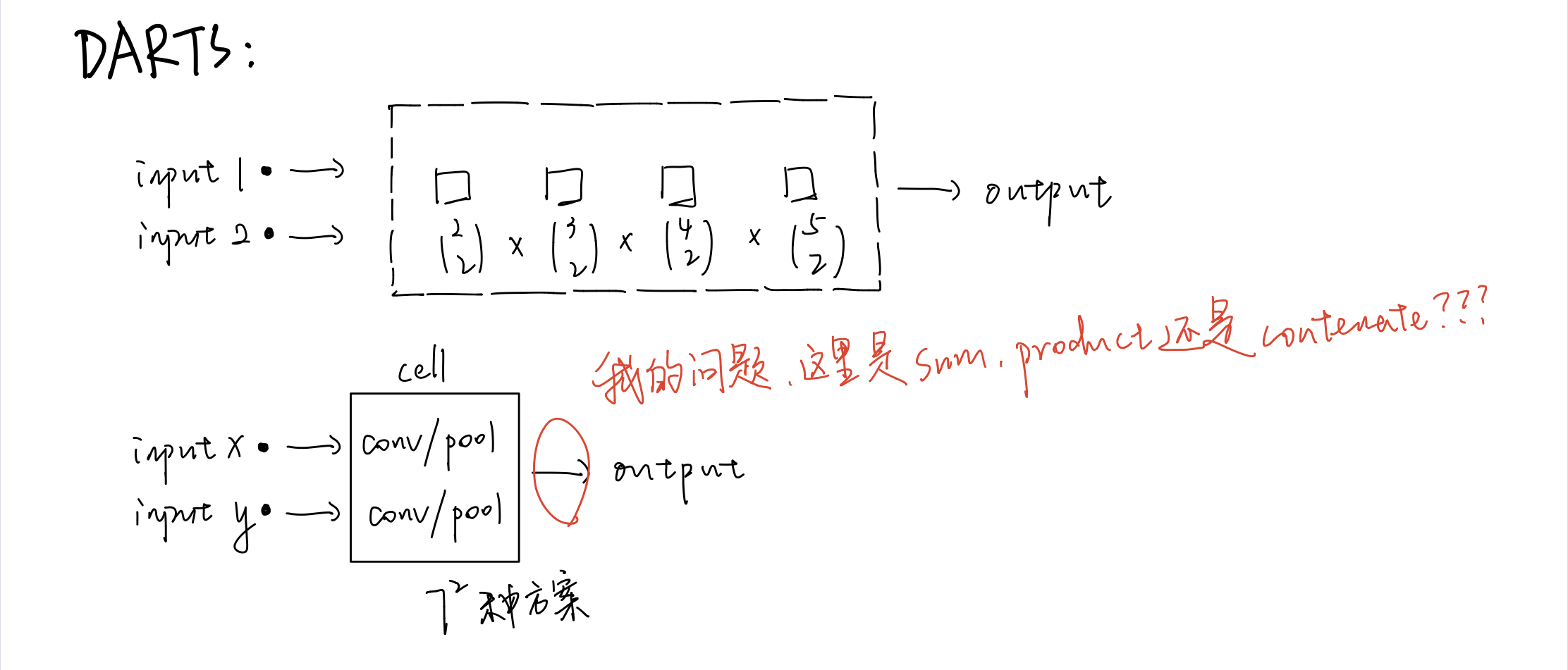
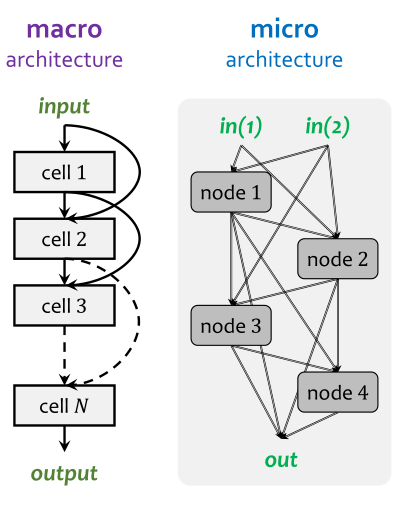
此类工作假设所有的cell都是相同结构，所以只需要搜索cell内部的operator即可，对应笔记2.2图中的 micro-NAS。假设输入是两个节点（index 为 -2 -1）而其余的N个节点可分为 C1个 connection node ( dil-conv-3x3空洞卷积, sep-conv-5x5分组卷积, identity, max-pool-3x3 ) 和 C2 个 summarization function node ( sum, concat, product )。最重要的约束条件是 Each hidden node is connected to two nodes with smaller indices 以及 The outputs of all intermediate nodes are concatenated into the output of the cell。

假设一个 cell 里有 C3 topologies，意味着： \(C_3 = \bigl( \begin{smallmatrix} 2\\2 \end{smallmatrix} \bigr) \times \bigl( \begin{smallmatrix} 3\\2 \end{smallmatrix} \bigr) \times ... \times \bigl( \begin{smallmatrix} N+1\\2 \end{smallmatrix} \bigr)\) 这么来的：

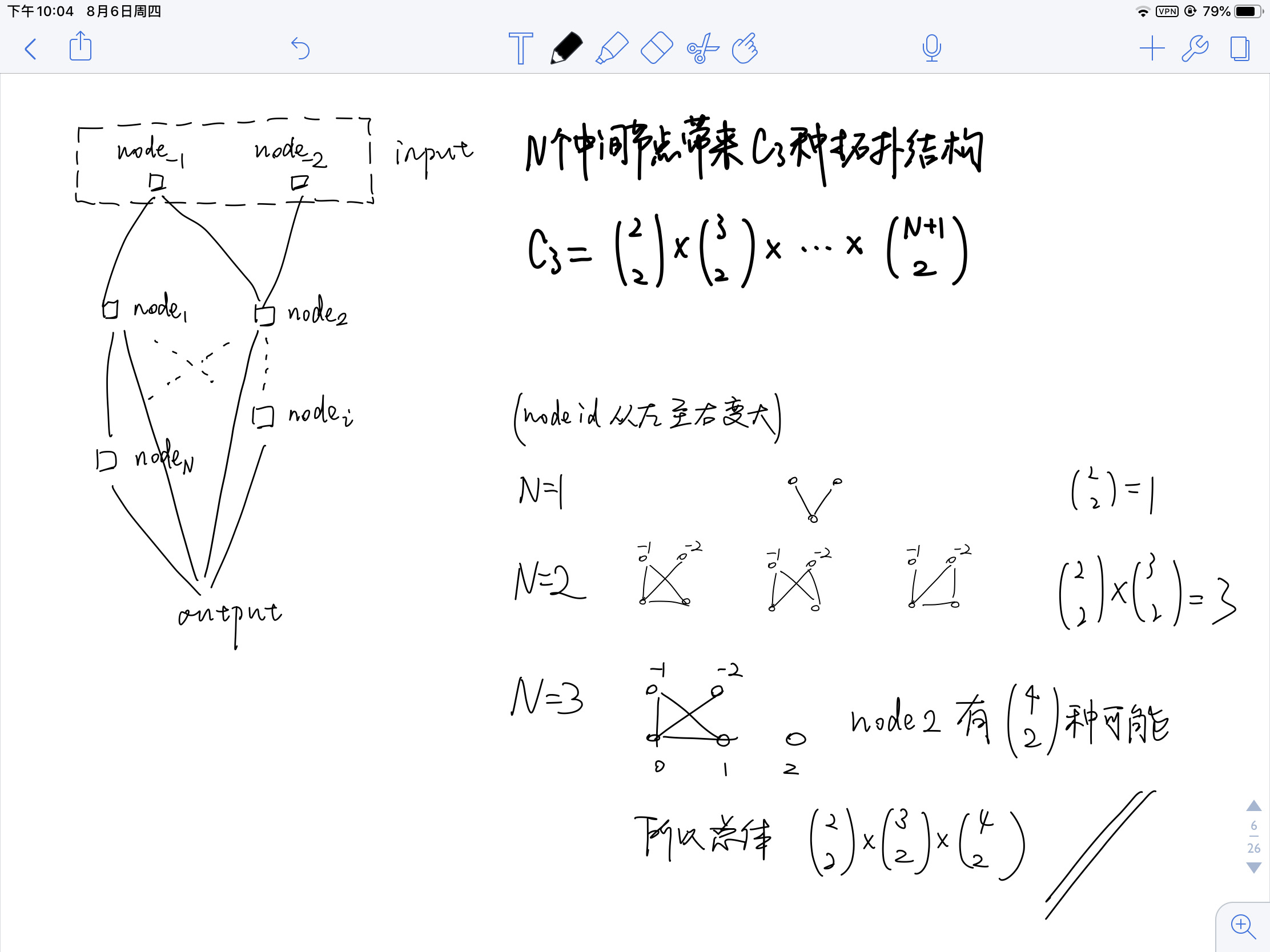
所以 cell 内部结构总共有： \((C_1^2 \times C_2)^N \times C_3\) 种可能。

这么来的每个输入都需要经过一个运算符得到一组特征，该运算符有C1种可能：

2.2.4 The DARTS Search Space

[27] K. Bi, L. Xie, X. Chen, L. Wei, and Q. Tian, “Gold-nas: Gradual, one-level, differentiable,” arXiv preprint arXiv:2007.03331, 2020. 这是 Lingxi Xie 在 VALSE2020 提到的工作

[48] A. Zela, T. Elsken, T. Saikia, Y. Marrakchi, T. Brox, and F. Hutter, “Understanding and robustifying differentiable architecture search,” in International Conference on Learning Representations, 2020.

[49] H. Zhou, M. Yang, J. Wang, and W. Pan, “Bayesnas: A bayesian approach for neural architecture search,” in International Conference on Machine Learning, 2019.

[50] M. Cho, M. Soltani, and C. Hegde, “One-shot neural architecture search via compressive sensing,” arXiv preprint arXiv:1906.02869, 2019.

[51] L. Wang, L. Xie, T. Zhang, J. Guo, and Q. Tian, “Scalable nas with factorizable architectural parameters,” arXiv preprint arXiv:1912.13256, 2019.

[52] K. Bi, C. Hu, L. Xie, X. Chen, L. Wei, and Q. Tian, “Stabilizing darts with amended gradient estimation on architectural parameters,” arXiv preprint arXiv:1910.11831, 2019.

C1 有 7 种选择方案。引入了一个 dummy-zero operator 参与搜索，但是不会出现在最终的 architecture 内。

sep-conv-3x3, sep-conv-5x5, dil-conv-3x3, dil-conv-5x5, max-pool-3x3, avg-pool-3x3, skip-connect

为了让架构搜索更容易 differentiable，每层的输入数据可以来自前层输出的任意两个。

”To ease the formulation of differentiable architecture search, each layer receives input data from an arbitrary number of previous layers in the same cell though only two of them are allowed to survive.“

接下来作者给出了一道计算题：

Provided that 4 intermediate cells are present, the number of architectures for both the normal and reduction cells is \(\bigl( \begin{smallmatrix} 2\\2 \end{smallmatrix} \bigr) \times \bigl( \begin{smallmatrix} 3\\2 \end{smallmatrix} \bigr) \times \bigl( \begin{smallmatrix} 4\\2 \end{smallmatrix} \bigr) \times \bigl( \begin{smallmatrix} 5\\2 \end{smallmatrix} \bigr) \times 7^8 \approx 1.0 \times 10^9\) 这么来的：

and the entire space has around \(1.1 \times 10^{18}\) architectures.

这个数怎么来的我就不知道了，可能得看一下原论文。

2.2.5 The MobileNet Search Space

[139] M. Tan, B. Chen, R. Pang, V. Vasudevan, M. Sandler, A. Howard, and Q. V. Le, “Mnasnet: Platform-aware neural architecture search for mobile,” in Computer Vision and Pattern Recognition, 2019.

[143] M. Tan and Q. V. Le, “Efficientnet: Rethinking model scaling for convolutional neural networks,” in International Conference on Machine Learning, 2019.

[144] X. Chu, B. Zhang, R. Xu, and J. Li, “Fairnas: Rethinking evaluation fairness of weight sharing neural architecture search,” arXiv preprint arXiv:1907.01845, 2019.

[145] M. Tan and Q. V. Le, “Mixconv: Mixed depthwise convolutional kernels,” in British Machine Vision Conference, 2019.

[151] J. Fang, Y. Sun, Q. Zhang, Y. Li, W. Liu, and X. Wang, “Densely connected search space for more flexible neural architecture search,” in Computer Vision and Pattern Recognition, 2020.

[161] J. Mei, Y. Li, X. Lian, X. Jin, L. Yang, A. Yuille, and J. Yang, “Atomnas: Fine-grained end-to-end neural architecture search,” in International Conference on Learning Representations, 2020.

[162] S. Chen, Y. Chen, S. Yan, and J. Feng, “Efficient differentiable neural architecture search with meta kernels,” arXiv preprint arXiv:1912.04749, 2019.

[170] Y. Li, X. Jin, J. Mei, X. Lian, L. Yang, C. Xie, Q. Yu, Y. Zhou, S. Bai, and A. L. Yuille, “Neural architecture search for lightweight non-local networks,” in Computer Vision and Pattern Recognition, 2020.

[173] R. Guo, C. Lin, C. Li, K. Tian, M. Sun, L. Sheng, and J. Yan, “Powering one-shot topological nas with stabilized share-parameter proxy,” in European Conference on Computer Vision, 2020.

[343] A. Howard, M. Sandler, G. Chu, L.-C. Chen, B. Chen, M. Tan, W. Wang, Y. Zhu, R. Pang, V. Vasudevan et al., “Searching for mobilenetv3,” in Computer Vision and Pattern Recognition, 2019.

cell 数固定，但是 cell 之间的 skip-connection 被取消，参考 MobileNet V1 只保留单链，但是 cell 内部的 layer number 是可以被搜索的。

2.2.6 Other Search Spaces

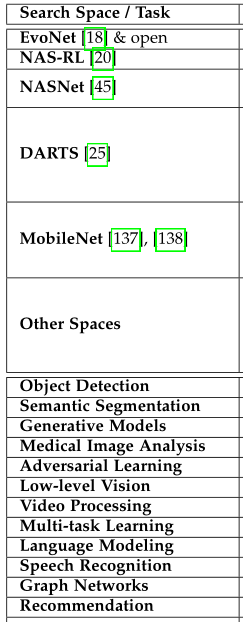
Table 1 提到了不同任务的NAS方法，但似乎都是2D-CNN的。

2.3 Search Strategy and Evaluation Method

2.3.1 Individual Heuristic Search Strategies

启发式搜索策略:= 每次对架构进行采样遵循概率函数 p，训练采样网络得到对应的 performance，再通过启发式算法对 p 进行更新。通常的想法是如果一个架构的 performance 高，那么理论上与其类似的 architecture 都可以达到同等 performance。当 p 的更新与采样网络的 performance 变得没有关联（启发式算法不“收敛”）时，启发式采样就退化为随机采样了。

• genetic algorithm or evolutionary algorithm: 通过遗传算法搜索架构的过程包括论 crossover, mutation, selection 和 elimination
• reinforcement learning

启发式搜索的缺点就是计算量太大，采样得到的每个网络都得 train to converge。

2.3.2 Weight-Sharing Heuristic Search Strategies

super-network & sub-architecture: 权重共享NAS的动机是优化整个超网的参数，而不是为了使得采样的子网络不断取得更高的 performance。

It is worth emphasizing that sampling a sub-architecture with the weights directly copied from the super-network does not reflect its accurate performance on the validation set, because the weight-sharing training procedure was focused on optimizing the super-network as an entire but not the individual sub-architectures.

但是采样子网络的时候依然需要采用启发式搜索。

2.3.3 Weight-Sharing Differentiable Search Strategies

在目标函数中优化了 Architectural Parameters —— modeling the likelihood that the candidate edges and/or operators are preserved in the final architecture。此时 heuristic search 变成了 differentiable search。

着重介绍了 DARTS 的训练过程，给出了 training scheme。

缺点是不鲁棒，收敛困难，每次训练得到的子网络可能差别很大。

2.3.4 Predictor-Based Search Methods

NAS-Bench-101 等 Benchmark 给出了 SOTA 网络的可能架构，所以可以训练一个 network predictor，输入是网络架构的编码，输出是该网络的 performance。

2.4 Summary

在《Best practices for scientific research on neural architecture search》提出了NAS论文应该涉及的内容，包括如何做 ablation, 以及这里的所有问题。

3 TOWARDS STABILIZED WEIGHT-SHARING NAS

3.1 An Alternative Formulation of Weight-Sharing NAS

假设我们为每个 candidate sub-network 学习一个编码 α（该编码也可以表示全网），sub-network 的权重参数为 ω，则 super-network 可以表示为： \(\bf{y} = \bf{F(x;\alpha,\omega)}\) 权重共享的NAS目标函数为：

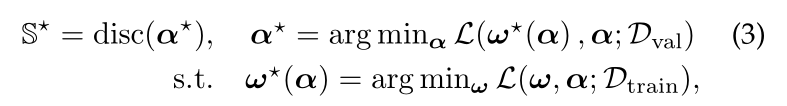
disc() 函数表示对可微的 α 进行离散化（比如 out_channels=5.6 –> out_channels=5）

3.2 The Devil Lies in the Optimization Gap

作者定义的 optimization gap —— well-trained super-network 不一定可以通过权重共享架构搜索（不论是启发式搜索还是可微搜索）得到 high-quality sub-architecture。

我们定义一种评估子网络性能的方法：对于在数据集D上搜索到的网络架构\Bbb{S}， \(\text{Eval}(<\Bbb{S},ω(\Bbb{S})>|D_{\text{val}}) = 1 − L(\omega^*(\alpha),\alpha;D_{\text{val}})\) Optimization Gap 带来了一种噪声\epsilon，使得搜索到的架构 \(\epsilon(\alpha)\) 往往会有 \(|\text{Eval}(\epsilon(\alpha_1)) - \text{Eval}(\epsilon(\alpha_2))| > |\text{Eval}(\alpha_1) - \text{Eval}(\alpha_2)|\) 并且即使搜索到的两个架构拓扑类似，在验证集上表现差不多，re-train后在测试集上的精度也可能大不同。

权重共享启发式搜索

权重共享启发式搜索需要每次从全网中采样一个子网络出来，然后通过启发式搜索确定采样概率。而启发式策略是通过对子网络进行训练，以验证集精度作为指标。但是研究发现子网络的验证集精度（val acc）与该网络 re-train 之后的测试集精度（test acc）没有相关性，Kendall相关系数几乎为0。

在统计学中，Kendall相关系数是以Maurice Kendall命名的，并经常用希腊字母τ表示其值。肯德尔相关系数是一个用来测量两个随机变量相关性的统计值。一个肯德尔检验是一个无参数假设检验，它使用计算而得的相关系数去检验两个随机变量的统计依赖性。

1. 如果两个属性排名是相同的，系数为1 ，两个属性正相关。
2. 如果两个属性排名完全相反，系数为-1 ，两个属性负相关。
3. 如果排名是完全独立的，系数为0。

本工作作者认为一种可能原因是每轮搜索都只是优化全网的一部分，因此在 final iteration 采样得到的子网络们，其精度主要取决于在之前轮次出现的频率。原文这么说的：

This is partly due to the strategy that optimizes part of the super-network in each iteration, so that whether a sub-architecture performs well in the final evaluation depends on the frequency that it appears, in particular the final iterations of the training procedure. This is mostly random and uncontrollable.

权重共享可微搜索

For weight-sharing differentiable search, the optimization gap can be quantified by observing the accuracy of the optimal sub-architecture without re-training the network weights, ω .

3.3 Shrinking the Optimization Gap

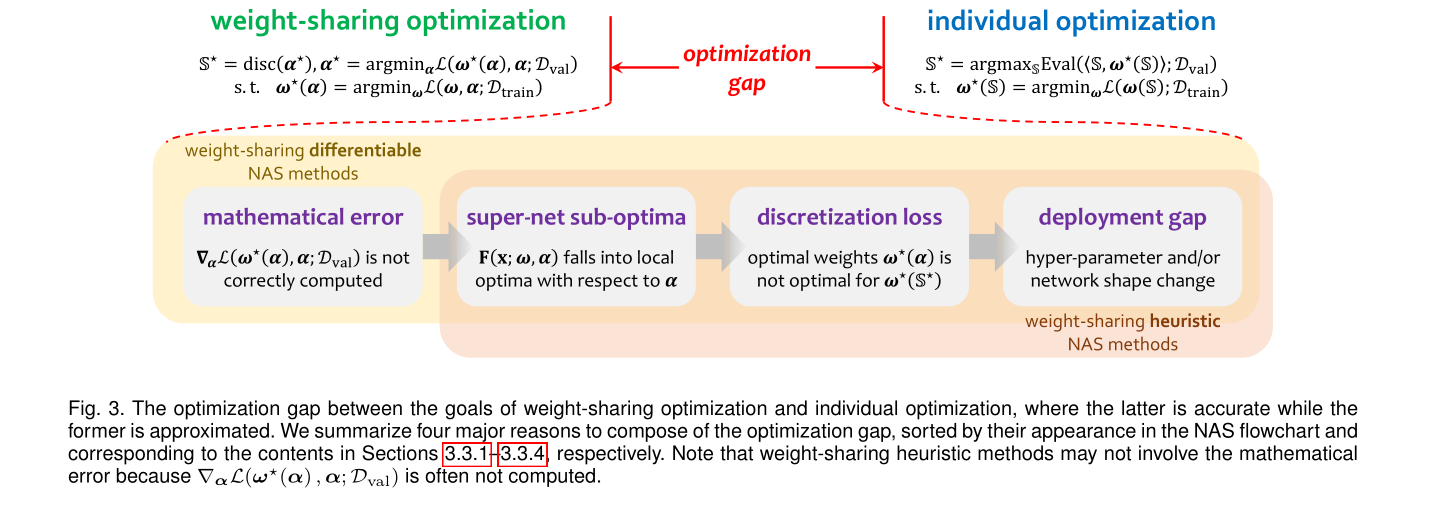
这里的 individual optimization 指的是传统的端到端训练，weight-sharing optimization 指的是每次指优化子网络的参数，最终目的是得到一个 well-trained super-network。

我的问题：这个gap和3.2节定义的gap好像不是一个东西…

1. mathematical error: 对于 architecture param 的梯度不准，而且 \alpha 参数通常只有千量级但是 \omega 有百万量级，参数空间不同，所以训练到同时收敛会比较困难。
2. super-net-sub-optima: \alpha 和 \omega 的协同优化困难，目标函数可能收敛到 local minimum。
3. discretization loss: discretization (离散化) 可能带来意外的精度跳水。
4. deployment gap: There are some differences in the network shape or hyper-parameters between the search and evaluation phases, making the searched architecture difficult in deployment. 搜索阶段通过超参数集A得到的最优子网络，在re-train过程中往往不可以用。因此为了在最优子网络下得到最好的权重参数，就得炼丹，这就不够 autoML 了。

于是本节 review 了针对以上四个问题的解决方案。

3.3.1 Fixing the Mathematical Error

背景知识: Hessian 矩阵

百度百科里的 Hessian 矩阵：

DARTS 公式推导

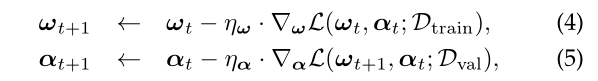
DARTS的训练要求 \(ω_{t+1} = ω^*(α_t)\) 当权重参数 \omega 的参数空间巨大时，\omega_{t+1} 很难简单地训练到最优。

此外，作者也提及了结构参数 \alpha 的梯度虽然是精确计算的 (accurately computed) 但是是 computationally intractable 的 (涉及到计算 \omega 的 inverse Hessian matrix)。没毛病，因为 \omega_{t+1} 也是通过梯度计算得到的，所以计算 \alpha_{t+1} 相当于计算了一次二阶梯度。

以下是DARTS原文的公式推导，和上面(4)(5)式是一个意思：

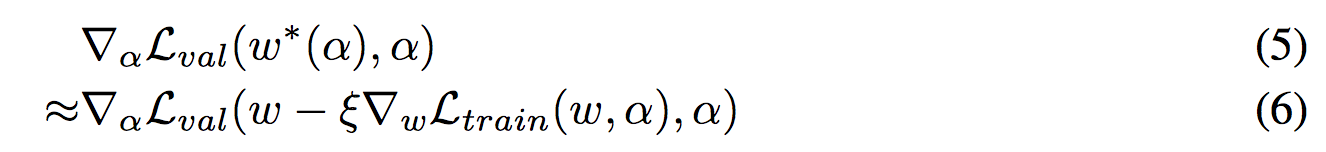
因为出现了 Hessian 二阶矩阵，所以又提出了近似算法：

这个近似算法的问题在于 The solution that DARTS used is to ignore the optimality of ω_{t+1} and use the identity matrix to approximate the inverse Hessian matrix of ω. (没看懂)

这个近似算法是错的，很容易带来模式坍缩 (mode collapse)，有点类似GAN的模型坍缩，表现在得到的子网络中存在太多的skip-connection结构，而且 performance 不好。为避免模式坍缩，有工作在DARTS基础上提出了 early termination 和 constrain the property of the sub-architecture (添加对各个结构的约束条件) 两种解决方案。但是这些解决方案都存在训练不稳定的问题，本篇综述的作者认为此类NAS有20%~80%的机率不会收敛到最优。

early termination 在文章《DARTS+: Improved Differentiable Architecture Search with Early Stopping》 中被提出。 早停准则：当各个可学习算子（比如卷积）的 alpha (表示算子出现在最终架构里的概率) 排序足够稳定（比如 10 个 epoch 保持不变）的时候，搜索过程停止。

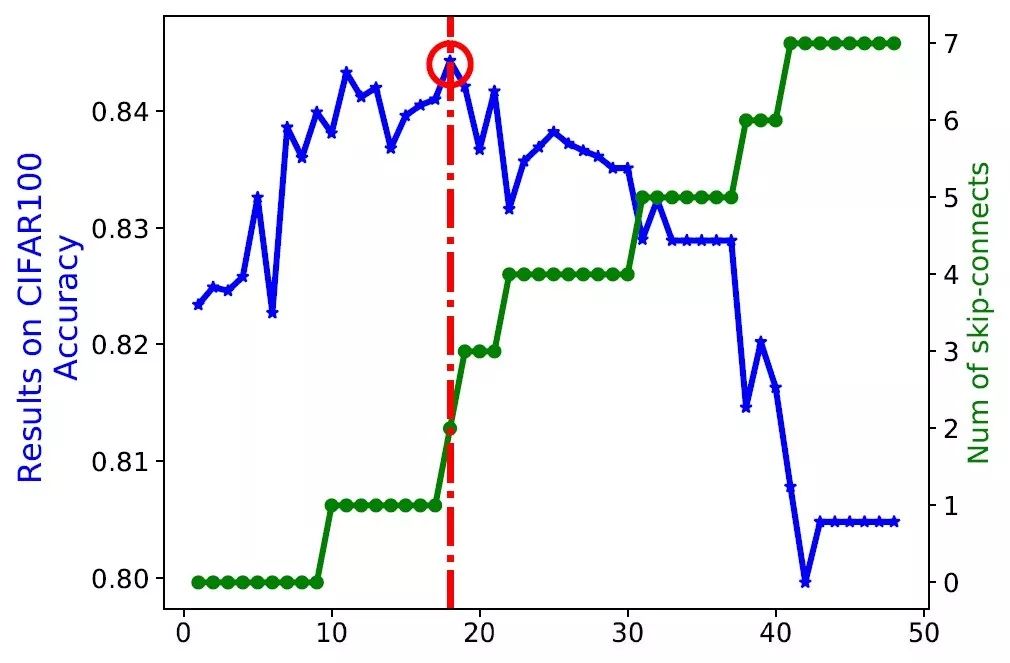
模式坍缩：随着搜索轮次增加，skip-connection结构数增加，CIFAR100精度降低。这是DARTS算法的主要问题。

DARTS 两步NAS算法的优化 (bi-level optimization)

1. using a better approximation to achieve an estimation error bound [52]
2. applying adversarial perturbation as regularization to smooth the search space [113]
3. applying mixed-level optimization to bypass the dramatic approximation [114]

但是以上方法都是 ad-hoc 的，不能完全解决两步NAS算法二阶优化 error 大的问题。于是提出了一步NAS算法。

DARTS升级—— 一步NAS算法 (one-level optimization)

一步NAS意味着不需要根据验证集去更新网络结构参数 \alpha，而是只在训练集上同时更新权重参数\omega和结构参数\alpha。也就是说：

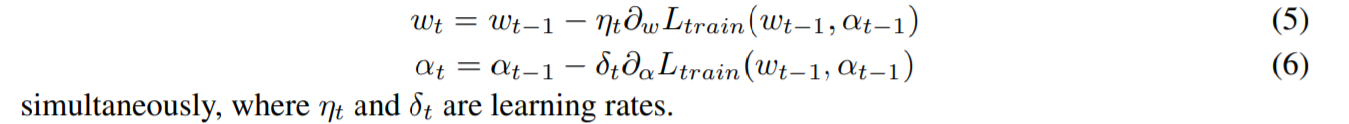
但是由于二者参数空间大小不同 (\omega参数空间远大于\alpha)，所以优化是困难的。本篇综述的作者认为一步NAS会为\omega带来bias，也就是训不好。具体方案包括：

Researchers proposed to partition the operator set into parameterized (各种卷积) and non-parameterized (池化/skip-connection) groups to facilitates the fair comparison between similar operators [97].

[97] G. Li, X. Zhang, Z. Wang, Z. Li, and T. Zhang, “Stacnas: Towards stable and consistent optimization for differentiable neural architecture search,” arXiv preprint arXiv:1909.11926, 2019.

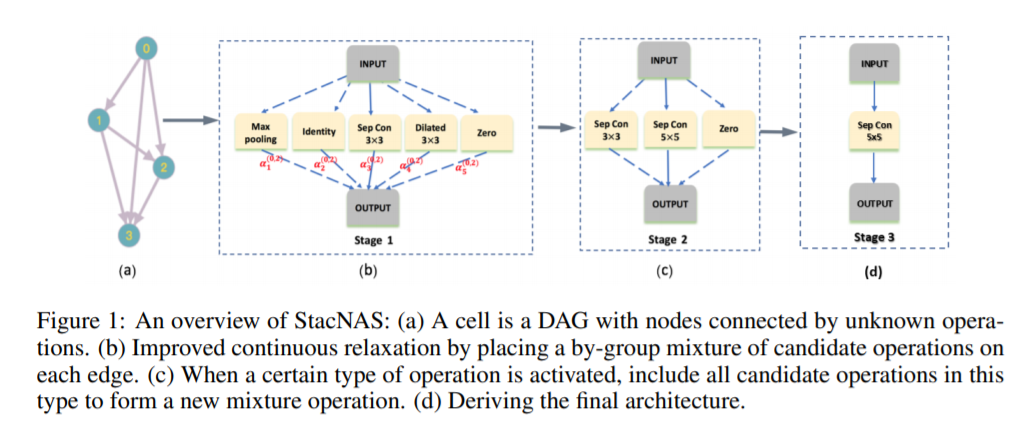
StacNAS这个工作的主要贡献 —— 如图，将所有算子分组（池化一组，分组卷积一组，identity一组，空洞卷积一组），首先判定组算子出现的概率，确定下哪一组算子应该保留（图中保留下来了分组卷积这一组）；然后判定该组算子内到底应该将哪一个（3x3；5x5）加入最终结果中。

A more elegant solution is provided by [27] which shows that simply adding regularization (e.g., data augmentation [401] or Dropout [402]) or using a larger dataset (e.g., ImageNet [39]) in the search procedure is sufficient to balance α and ω and improve one-level optimization.

[27] K. Bi, L. Xie, X. Chen, L. Wei, and Q. Tian, “Gold-nas: Gradual, one-level, differentiable,” arXiv preprint arXiv:2007.03331, 2020.

3.3.2 Avoiding the Sub-Optima of Super-Network

super-network 训练初期阶段很容易为 池化/skip-connection 等不带参数的算子 (相对于卷积) 赋予更大的权值，因为此类算子没有参数所以更好优化。所以就使得super-network无法训练到全局最优。

一种思路是在训练初期固定网络架构，使得网络权值参数可以更好地初始化，本篇综述的作者称此类方法为“warm up the search procedure”。其中包括

1. 在两步NAS算法中，freezing the update of α in the starting stage and allowing ω (mostly the weights of all convolution operators) to be well initialized. [26], [81], [82], [109]
2. 在启发式NAS算法中，performing fair sampling [142], [144] for super-network training followed by a standalone sampling procedure starting with a uniform distribution on \Bbb{S}.
3. partitioning the operators into parameterized and non-parameterized groups to avoid unfair competition [97], [235]
4. using operator-level Dropout to weaken the superiority of non-parameterized operators [81]
5. dynamically adjusting the candidate operator set to allow some perturbation in \Bbb{S} [82].

3.3.3 Reducing the Discretization Loss

对连续可微的 α 进行离散化（比如 out_channels=5.6 –> out_channels=5）会带来意外的精度损失。解决方案如下:

1. First, converting α from continuous to discrete so that the search procedure is always optimizing the discretized sub-architectures. This strategy is used in both heuristic [142], [144] and differentiable [78], [86], [93] search methods, and it can be interpreted as a kind of super-network regularization.

2. Second, pushing the values of α towards either ends (概率为0或者1) so that the eliminated elements have very low weights [88], [101], [133].

   [88] A. Noy, N. Nayman, T. Ridnik, N. Zamir, S. Doveh, I. Friedman, R. Giryes, and L. Zelnik, “Asap: Architecture search, anneal and prune,” in International Conference on Artificial Intelligence and Statistics, 2020.

   [101] X. Chu, T. Zhou, B. Zhang, and J. Li, “Fair darts: Eliminating unfair advantages in differentiable architecture search,” in European Conference on Computer Vision, 2020.

   [133] Y. Tian, C. Liu, L. Xie, J. Jiao, and Q. Ye, “Discretization-aware architecture search,” arXiv preprint arXiv:2007.03154, 2020.

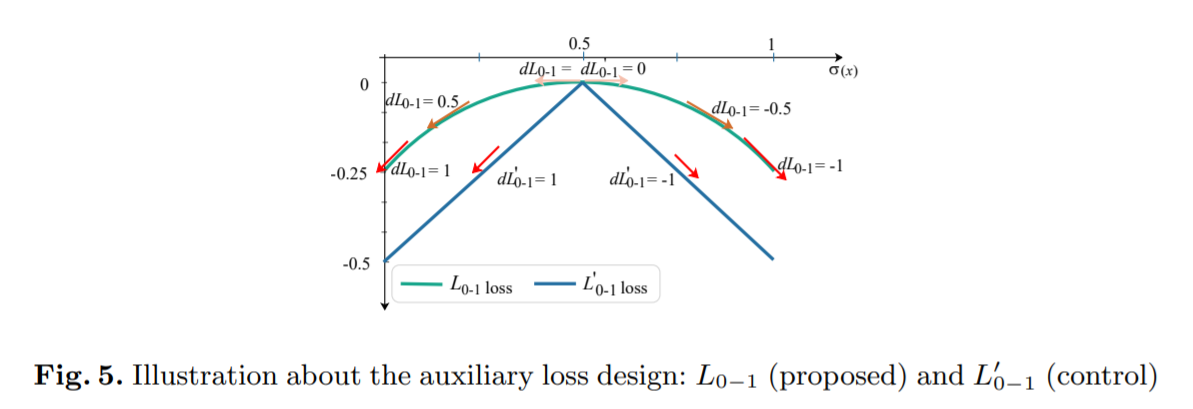
   没看懂。所以扫了其中一篇文章《Fair DARTS》: 目前认为主要两个贡献 1) 把 softmax 换成 sigmoid; 2) 提出01损失函数 (zero-one loss) to push the sigmoid value of architectural weights towards 0 or 1.

   

   

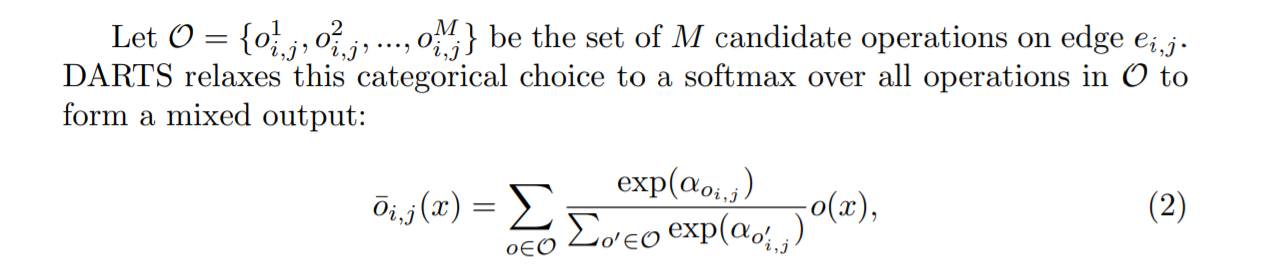
   01损失函数的设计动机：To achieve our goal, the loss design f(z) must meet three basic criteria：

   1. It needs to have a global maximum at z = 0.5 and a global minimum at 0 and 1. 为什么全局最大值呢要限制在0.5呢？
   2. The gradient magnitude df dz/z≈0.5 has to be adequately small to allow architectural weights to fluctuate, but large enough to attract z towards 0 or 1 when they are a bit far from 0.5.
   3. It should be differentiable for backpropagation.

   

   

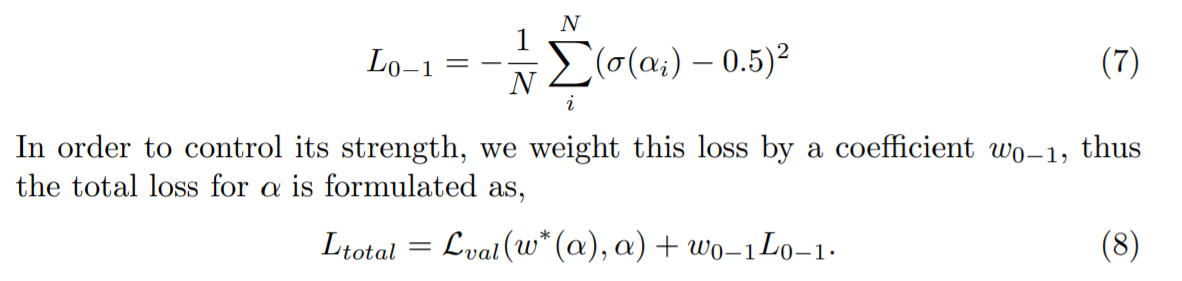
3. Third, weakening one-time discretization as gradual network pruning [27], [88], [94], [102] so that the super-network is not pulled too far from the normal status ( ω is close to the optimum) and recovers after some training epochs (before the next pruning operation). 就是搜索过程中对超网进行剪枝，调整参数空间减少离散化出错的概率。

   [27] K. Bi, L. Xie, X. Chen, L. Wei, and Q. Tian, “Gold-nas: Gradual, one-level, differentiable,” arXiv preprint arXiv:2007.03331, 2020.

   [88] A. Noy, N. Nayman, T. Ridnik, N. Zamir, S. Doveh, I. Friedman, R. Giryes, and L. Zelnik, “Asap: Architecture search, anneal and prune,” in International Conference on Artificial Intelligence and Statistics, 2020

   [94] X. Zheng, R. Ji, L. Tang, Y. Wan, B. Zhang, Y. Wu, Y. Wu, and L. Shao, “Dynamic distribution pruning for efficient network architecture search,” arXiv preprint arXiv:1905.13543, 2019.

   [102] G. Li, G. Qian, I. C. Delgadillo, M. Muller, A. Thabet, and B. Ghanem, “Sgas: Sequential greedy architecture search,” in Computer Vision and Pattern Recognition, 2020.

3.3.4 Bridging the Deployment Gap

[81] X. Chen, L. Xie, J. Wu, and Q. Tian, “Progressive differentiable architecture search: Bridging the depth gap between search and evaluation,” in International Conference on Computer Vision, 2019.

在文章 [81] 中作者发现给定一个搜索到的最优子网络A，增加深度 aka Cell数 可增加模型精度；但是在深度固定为A的深度时，搜索到的最优子网络B和子网络A会差很多，作者称其为 depth gap，并提出了一个 progressive 解决方案 P-DARTS。

P-DARTS 论文笔记: https://www.cnblogs.com/marsggbo/p/12231093.html

PDARTS提出在搜索过程中逐渐增加网络层数，随之而来的问题以及解决办法分别是：

1. 计算量增大：当层数增加后，计算量也会成倍增加。因此为了解决这个问题，PDARTS提出了search space approximation策略，即每当层数增加时就会相应地减少候选操作的数量。
2. 稳定性降低：在搜更深的网络时，skip-connection会占据主导地位，这对模型稳定性有较大影响。解决办法是对搜索空间做正则化约束(search space regularization)：
   • operation-level Dropout，来避免skip-connection占主导地位
   • 在evaluation过程中控制skip-connection的出现次数

文章 [81] 和启发式搜索的思路是不同的，启发式搜索往往在超网中采样指定拓扑结构的网络，但是该工作是递进增加子网络的深度（如图是 Normal Cell 个数1–>3–>5）。

在本笔记3.3节开头，作者对Deployment Gap的定义是——搜索阶段通过超参数集A得到的最优子网络，在re-train过程中往往不可以用。因此为了在最优子网络下得到最好的权重参数，就得炼丹，这就不够 autoML 了。但是工作 [81] 和这个 gap 好像没关系……

Despite the progressively growing super-network [81], a more essential solution to the depth gap is to directly search in the target network shape. This is natural for most heuristic search methods [139], [142], [144], [343] while the differentiable search methods can encounter the difficulty of training very deep super-networks – this is mainly due to the mathematical error [52] elaborated in Section 3.3.1.

Going one step further, researchers have been investigating the relationship between the shallow super-network and the deep sub-architectures [126], [166], [248], and a likely conclusion is that they can benefit from each other.

[126] H. Yu and H. Peng, “Cyclic differentiable architecture search,” arXiv preprint arXiv:2006.10724, 2020.

[166] S.-Y. Huang and W.-T. Chu, “Ponas: Progressive one-shot neural architecture search for very efficient deployment,” arXiv preprint arXiv:2003.05112, 2020.

[248] R. Meng, W. Chen, D. Xie, Y. Zhang, and S. Pu, “Neural inheritance relation guided one-shot layer assignment search,” arXiv preprint arXiv:2002.12580, 2020.

在本小节综述作者又提到了 optimal sub-architecture 的 transferability（ImageNet –> COCO/PASCAL VOC），这也是个 deployment gap。但是如何提高 subnet 的 transferability 仍属于未知的领域。

An example is that EfficientDet is difficult to be trained yet does not show dominating detection accuracy, although it borrows the architecture and pre-trained weights from EfficientNet [143], the state-of-the-art image classification architecture.

3.3.5 Learning-based Approaches

具体方法是 encode each sub-architecture into a vector and then use a model to predict the accuracy explicitly。在 2.3.4 小节提到了以 NAS-Benchmark 为基准训练 predictor 的方法，但是本小节提出的方法是利用 predictor 优化超网的参数 (embedded into the search procedure to guide the super-network optimization [166], [171], [367]) 同时减少超网参数空间、加速搜索 (filter out weak candidates earlier and thus accelerate the search procedure [74], [121])。

3.4 Unsolved Problems

问题一：最优子结构的 neighbor 是否也是优秀的子网络呢？如果是的话，搜索空间就很有可能是平滑的。如果不是，那么如何定义一个平滑的搜索空间便于优化呢？

问题二：

权重共享NAS对每个算子的打分criterion（对应DARTS算法里的\alpha）是公平的吗？

Second, weight-sharing NAS methods facilitate different operators and connections to compete with each other, but it is unknown if the comparison criterion is made fair. For example, almost all search spaces involve the competition among convolutions with various kernel sizes (e.g., 3 × 3 vs. 5×5 or 7×7 ), and sometimes, network compression forces competition among different channel and/or bit widths. Although the ‘heavy’ operators are intuitively stronger than the ‘light’ operators, they often suffer slower convergence during the training procedure. That is to say, the search result is sensitive to the time point that comparison is made between these operators. This can cause considerable uncertainty especially in very large search spaces.

问题三：

权重共享NAS是通过大超网找最优子网络，能否从一个相对小的超网开始搜索，得到一个大的最优网络呢？（个人认为是一个相对于 pruning 的 growing 过程）

更完整的故事：开局一个小超网，在超网上一边搜索最优子网络，一边增大（原文称作extent the search space）超网的拓扑结构，最后得到一个比初始超网大，但是比最终超网小的最优子网络。

4 RELATED RESEARCH DIRECTIONS

4.1 Model Compression

提到了剪枝与量化，这里只复制下剪枝+NAS点名的文章：

[244] R. Zhao and W. Luk, “Efficient structured pruning and architecture searching for group convolution,” in International Conference on Computer Vision Workshops, 2019.

[359] X. Li, Y. Zhou, Z. Pan, and J. Feng, “Partial order pruning: for best speed/accuracy trade-off in neural architecture search,” in Computer Vision and Pattern Recognition, 2019.

[360] J. Yu and T. Huang, “Network slimming by slimmable networks: Towards one-shot architecture search for channel numbers,” arXiv preprint arXiv:1903.11728, 2019.

[364] X. Dong and Y. Yang, “Network pruning via transformable architecture search,” in Advances in Neural Information Processing Systems, 2019.

[418] Y. He, J. Lin, Z. Liu, H. Wang, L.-J. Li, and S. Han, “Amc: Automl for model compression and acceleration on mobile devices,” in European Conference on Computer Vision, 2018.

[419] X. Xiao, Z. Wang, and S. Rajasekaran, “Autoprune: Automatic network pruning by regularizing auxiliary parameters,” in Advances in Neural Information Processing Systems, 2019.

提出了NAS的一个未来方向 —— 软硬件协同设计，并点名了以下文章：

[432] H. Cai, J. Lin, Y. Lin, Z. Liu, K. Wang, T. Wang, L. Zhu, and S. Han, “Automl for architecting efficient and specialized neural networks,” IEEE Micro, vol. 40, no. 1, pp. 75–82, 2019.

[433] Q. Lu, W. Jiang, X. Xu, Y. Shi, and J. Hu, “On neural architecture search for resource-constrained hardware platforms,” arXiv preprint arXiv:1911.00105, 2019.

[434] M. S. Abdelfattah, Ł. Dudziak, T. Chau, R. Lee, H. Kim, and N. D. Lane, “Best of both worlds: Automl codesign of a cnn and its hardware accelerator,” arXiv preprint arXiv:2002.05022, 2020.

[435] S. Gupta and B. Akin, “Accelerator-aware neural network design using automl,” arXiv preprint arXiv:2003.02838, 2020.

[436] W. Jiang, Q. Lou, Z. Yan, L. Yang, J. Hu, X. S. Hu, and Y. Shi, “Device-circuit-architecture co-exploration for computing in-memory neural accelerators,” IEEE Transactions on Computers, 2020.

[437] W. Jiang, L. Yang, E. H.-M. Sha, Q. Zhuge, S. Gu, S. Dasgupta, Y. Shi, and J. Hu, “Hardware/software co-exploration of neural architectures,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2020.

[438] W. Jiang, L. Yang, S. Dasgupta, J. Hu, and Y. Shi, “Standing on the shoulders of giants: Hardware and neural architecture co-search with hot start,” arXiv preprint arXiv:2007.09087, 2020.

[439] J. Lin, W.-M. Chen, Y. Lin, J. Cohn, C. Gan, and S. Han, “Mcunet: Tiny deep learning on iot devices,” arXiv preprin tarXiv:2007.10319, 2020.

4.2 Dynamic Routing Networks

点名了几篇文章，扫了下ECCV2018《Skipnet: Learning dynamic routing in convolutional networks》

损失函数： \(L_{\theta}(\mathbf{g}, \mathbf{X}) = \mathcal{L}(\hat{y}(\mathbf{X}, F_{\theta}, g), y) - \frac{\alpha}{N} \sum_{i=1}^N (1 - g_i) C_i\) 目标函数：

g 对应 gate module (每个residual block 都有自己的 gate network)

梯度：

其中包括复合函数链式法则： \(\nabla_{\theta} \log p_{\theta}(\mathbf{g} | \mathbf{X}) = \frac{1}{p_{\theta}(\mathbf{g} | \mathbf{X})} \nabla_{\theta} p_{\theta}(\mathbf{g} | \mathbf{X})\) 对于最终梯度表达式，左部分就可以看作监督学习损失函数的梯度，右部分就可以看作强化学习损失的梯度。

4.3 Meta Learning

As weight-sharing NAS methods become more and more popular, meta learning can be used for various purposes, including (i) enhancing the few-shot learning ability of NAS methods [125], [464], [465], (ii) allowing NAS methods to transfer to different tasks [403], [404], [405], and (iii) providing complementary information to shrink the optimization gap [237], [466].

[237] H.-P. Cheng, T. Zhang, Y. Yang, F. Yan, S. Li, H. Teague, H. Li, and Y. Chen, “Swiftnet: Using graph propagation as meta-knowledge to search highly representative neural architectures,” arXiv preprint arXiv:1906.08305, 2019

[466] A. Dubatovka, E. Kokiopoulou, L. Sbaiz, A. Gesmundo, G. Bartok, and J. Berent, “Ranking architectures using meta-learning,” arXiv preprint arXiv:1911.11481, 2019.

4.4 Hyper-Parameter Optimization

NAS is essentially a kind of HPO, i.e., the network architecture is encoded as a set of hyper-parameters.

During NAS training, it is always a good choice to minimize the loss function in a short period of time, but this does not hold for HPO training

The recent efforts to combine NAS and HPO [494] provided a promising direction.

[494] X. Dong, M. Tan, A. W. Yu, D. Peng, B. Gabrys, and Q. V. Le, “Autohas: Differentiable hyper-parameter and architecture search,” arXiv preprint arXiv:2006.03656, 2020

4.5 Automated Data Augmentation

没有提到NAS与ADA的关系。

提到了文章《AutoAugment》按照NAS的逻辑，去做数据增强策略的选择。

[401] E. D. Cubuk, B. Zoph, D. Mane, V. Vasudevan, and Q. V. Le, “Autoaugment: Learning augmentation policies from data,” in Computer Vision and Pattern Recognition, 2019.

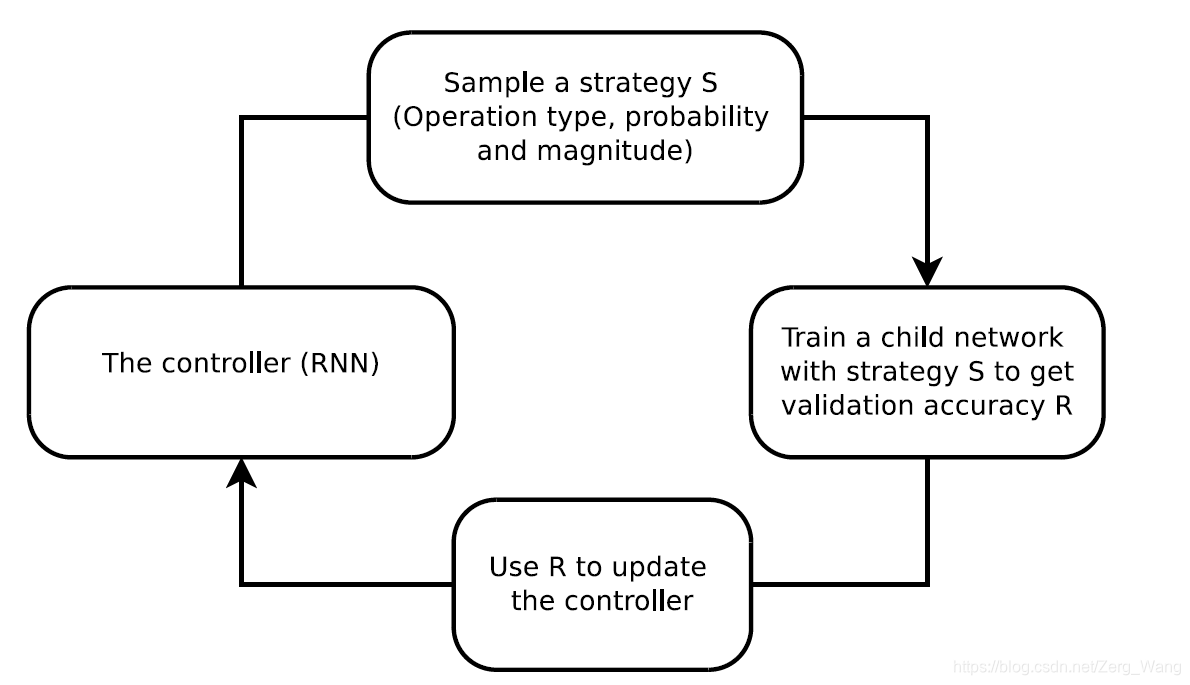
增强策略：多个子策略组成一个完整的增强策略。作者的实验中规定了每个完整策略由5个子策略构成。

子策略：由2个上文提到的增强操作组成，其中，每个操作由2个参数组成：probability和magnitude，分别是使用该操作的可能性以及该操作的使用幅度。不是所有的操作都需要magnitude，比如AutoContrast操作作者就规定其参数为0，但形式上这些操作仍会保留magnitude参数。此外，对于几何变换类的操作（Shear、Translate、Rotate），虽然有magnitude参数规定了操作幅度，但方向是随机的。例如旋转45度，在增强时可能会逆时针旋转45度，也可能顺时针旋转45度。

There is a survey [503] that reviews a wide range of data augmentation techniques for deep learning. Applying AutoML techniques for data augmentation was believed to have a high potential for future research.

[503] C. Shorten and T. M. Khoshgoftaar, “A survey on image data augmentation for deep learning,” Journal of Big Data, vol. 6, no. 1, p. 60, 2019